Тема 4. Поняття.
Загальна характеристика понять
В формальній логіці вважається, що елементарною формою мислення є поняття. Поняттям називається така форма мислення, яка відображає предмети, ознаки, а також відношення.
Наприклад, "людина", "праця", "краса" – це поняття, які відображають предмети. "Червоний", "прекрасне", "бути людиною" – ці поняття відображають ознаки. "Більше", "менше", "старший", „молодший” – в цих поняттях відображені певні відношення.
Головні характеристики поняття в формальній логіці – це зміст та об'єм. Під змістом поняття мається на увазі сукупність ознак, які мисляться в даному понятті. Ніяке поняття не може мислитися інакше як через певні ознаки. Адже ознаки – це те, за допомогою чого один предмет відрізняють від іншого, або завдяки чому предмети вважаються подібними.
Ще Арістотель звернув увагу, що не всі ознаки предмета є для нас однаково важливими. Він поділив їх на істотні, та неістотні. До істотних ознак він ознаки роду (для людини це буде приналежність до тваринного світу) та видової відмінності (для людини, скажімо, це здатність до мислення). Поєднання ознаки роду, та видової відмінності дає ще одну істотну ознаку – виду (людина – мисляча істота).
Об'єм поняття – це ті предмети, які охоплюються даним поняттям. Так об'єм поняття "людина", наприклад, складуть всі люди, які колись існували, існують зараз і ті, які коли-небудь будуть існувати.
Під предметом поняття мається на увазі будь-який його елемент, те що відображається в понятті.
Види понять.
За об'ємом всі поняття поділяються на одиничні та загальні. Виділяють деколи також поняття з так званими порожніми об'ємами. Маються на увазі ті поняття, які не мають відповідників в дійсності. Як приклад, приводяться поняття "кентавр", "бог" і т. п.
Одиничними називаються ті поняття, в яких мислиться тільки один предмет. Наприклад, поняття "Сонце", чи "Сократ". Загальними називаються ті поняття, в яких ми маємо на увазі два і більше предметів. Всі предмети, які мисляться в понятті, тобто, складають його об'єм, утворюють певний клас предметів. Класи загальних понять здебільшого можуть бути поділені на підкласи. Наприклад, дерева бувають різними – хвойними (голонасінними) та листяними (покритонасінними). Найдрібнішою частинкою об'єму поняття є елементи. Це такі поняття, які не можна поділити, щоб при цьому не втратились ознаки всього класу понять. Може здатися, що елементами, скажімо, поняття "комп'ютер" є поняття "монітор", чи, скажімо, "клавіатура". Насправді це не так. "монітор" не є елементом поняття "комп'ютер", тому, що він не має ознак комп'ютера, не може виконувати його функцій. Іншими словами, монітор - це не комп'ютер, точно так же, як, припустимо, голова людини – це ще не людина.
Серед загальних виділяють так звані всезагальні поняття, або категорії. До них відносять, як правило філософські поняття, такі як "матерія", "свідомість", "відношення", "час", "простір", "дія" і т. п. Формальна відмінність категорій від інших загальних понять полягає в тому, що їх об'єми не можуть бути включені в об'єми інших понять.
Загальні поняття можна поділити на реєструючі та нереєструючі поняття. Нереєструючими називають такі загальні поняття, в яких неможливо виділити окремі елементи. До них відносять, зокрема, назви речовин, матеріалів і т. п. Наприклад, вода, цукор, залізо, деревина, дощ, сніг і т. д. Зверніть увагу, що підкласи в цих поняттях можна виділити: наприклад, прісна і солона вода. Притому, підкласи теж виявляться збірними поняттями. Але елементи в збірних поняттях не виділяються. Як співається в відомій пісні "Одна дождинка, еще не дождь… Одна снежинка - еще не снег".
Відповідно, реєструючими називають загальні поняття, в яких можна виділити елементи. Наприклад, в понятті "дерево" (звичайно, коли ми маємо на увазі не матеріал, а різновид рослин) ми можемо помислити кожне дерево окремо, не втрачаючи при цьому ні одної суттєвої ознаки всього класу.
Не можна плутати граматичні форми однини та множини з одиничними та загальними поняттями. Так, скажімо, поняття "дерево", хоч і виражається іменником в однині, буде загальним поняттям, оскільки під цим поняттям мається на увазі дуже багато предметів.
Можна виділити також окремий клас збірних понять. Це такі поняття, які відображають клас однорідних предметів, які разом складають єдине ціле, але при цьму кожний з цих предметів нек має ознак цілого. Наприклад: бібліотека складається з книжок, але кожна книжка не є бібліотекою. „Студентська група”, „сім’я”, „планетна система”, „ансамбль” і т. п. – ось приклади такого роду понять.
Збірні поняття відрізняються від загальних понять саме тим, що ознаки класу тут не прикладаються до кожного окремого елемента, з яких складається цей клас.
Треба мати на увазі, що одні і ті ж поняття можуть виступати як збірні і як загальні, залежно від контексту, в якому вони вживаються. Наприклад, поняття „ліс” буде збірним, коли мова йде про ліс як сукупність дерев чи партію пиломатеріалів, і загальним, коли важливо розрізняти хвойний ліс від листяного чи змішаного. Те ж саме – бібліотека. Одна річ, коли вона нас цікавить саме як книгозбірня, інша – коли мова йде про бібліотеку як певний заклад культури, коли маються на увазі різні бібліотеки: дитячі, дорослі, наукові і т.п.
Деколи загальні поняття, щоб відрізнити їх від збірних, називають подільними. Мається на увазі, що будь яке загальне поняття можна поділити на підкласи, чи елементи так, що кожен з них збереже ознаки всього класу, чого ніяк не можна зробити зі збірним поняттям.
За змістом поняття поділяють на конкретні та абстрактні. Під конкретними поняттями в формальній логіці розуміють поняття, що позначають предмети матеріального світу, осіб, факти, явища, події, стани, дії. Абстрактними називають ті поняття, які позначають властивості, якості, стани речей або їх дії, коли вони розглядаються окремо від речей. Наприклад поняття „вага”, „колір”, „об’єм”, „форма” будуть абстрактними. Але поняття „важкий”, „кольоровий”, „об’ємний”, „формальний” вважаються конкретними.
Треба зауважити, що поділ понять на конкретні та абстрактні носить чисто формальний характер. Він є пережитком дуалістичного розуміння природи мислення. Насправді будь яке поняття абстрактне за своєю природою, оскільки воно є продуктом абстрагування. В той же час, будь яке поняття, не перестаючи, звичайно, при цьому бути абстракцією, може стати конкретним, якщо воно правильно відображає сутність предмета в певній практичній ситуації.
Поняття поділяються на позитивні та негативні. В позитивних поняттях фіксується наявність тієї чи іншої якості у предмета, а відповідні негативні поняття вживаються для того, щоб показати що така якість у предмета відсутня. Так, наприклад, позитивним поняттям „страх”, „смерть”, „радісний” неважко підібрати негативні відповідники – „безстрашність”, „безсмертя”, „нерадісний”.
Виділяють також абсолютні та відносні поняття. Відносними є поняття, які не мисляться поза зв’язком з якимось іншим поняттям. Наприклад поняття „верх” немислиме без поняття „низ”, „віце-президент” без „президент”, „контрреволюція” без „революція”, „причина” без „наслідок” і т. п.
Абсолютними називають поняття, які позначають предмети, явища, чи ознаки, які буцім-то можуть мислитися самі по собі. Звичайно поділ понять на абсолютні та відносні сам по собі є дуже відносним. Абсолютних понять в прямому розумінні цього слова не буває. Скажімо, в деяких підручниках з логіки як пприклад абсолютного поняття приводиться поняття „дім” і говориться, що, мислячи про дім, ми можемо не думати ні про що інше. На перший погляд, це правильно. Але архітектору, чи будівельнику так не здасться. Дім він пов’яже з фундаментом, а фундамент з грунтом, на якому дім стоїть, так само звично, як пересічна людина пов’язує „верх” з „низом”, чи „батьків” з „дітьми”. Кінець кінцем, ніяке поняття не може мислитися інакше, як тільки через певну сукупність ознак, які належать цьому предметові.
Відношення між поняттями.
Ті поняття, які мають спільні ознаки в логіці називають порівнюваними. Поняття, для яких не можна встановити спільних ознак, називають непорівнюваними. Порівнювані поняття поділяються на сумісні (ті, які мають спільні елементи) і несумісні (у яких спільних елементів нема). Можна виділити три типи порівнюваності (тотожність, або рівнооб'ємність, підпорядкування та перетин) та чотири типи несумісності (несумісні поняття, які в той же час є непорівнюваними, протилежні поняття, суперечливі поняття, та співпідпорядковані).
Відношення між порівнюваними поняттями є відношенням між їх об'ємами. Об'єми ж понять можна уявити як певні множини предметів. Це дозволяє використати для унаочнення такого роду відношень між поняттями прийняті в теорії множин круги Ейлера.
Візьмемо, скажімо, відношення підпорядкування. Підпорядкування – це таке відношення між двома поняттями, коли об'єм одного з них повністю включається в об'єм іншого, але не вичерпує його. На діаграмі це буде виглядати так
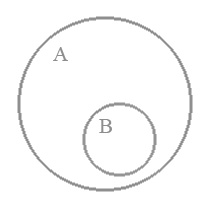
В даному випадку поняття А буде називатися підпорядковуючим, а поняття В – підпорядкованим. Те поняття, об'єм якого включає об'єм іншого поняття, називається підпорядковуючим, або інакше кажучи, родовим поняттям.
Підпорядкованим (видовим) називають те поняття, об'єм якого повністю входить в об'єм іншого поняття але не вичерпує його.
З точки зору змісту це означає, що будь-який елемент, чи підклас поняття має мати ознаки всього класу. Важливо не плутати відношення логічного підпорядкування з суспільними відносинами, службовими стосунками, відношенням частина-ціле, тощо. Скажімо може здатися, що до поняття генерал підпорядкованим буде поняття майор, лейтенант і т.д. Насправді, це неправильно. Ці поняття є несумісними, оскільки ні поняття майор, ні поняття лейтенант не входить до об'єму поняття генерал, простіше сказати, ні майор, ні лейтенант не є генералами. Підпорядкованими до поняття "генерал" були би тільки поняття "генерал-майор", "генерал-лейтенант".
Можливе таке відношення сумісності між двома поняттями, коли зміст їх різний, тобто вони характеризуються різними ознаками, але об'єми їх повністю співпадають, тобто вони означають одні і ті ж предмети. Такі поняття називаються тотожними, або рівнооб'ємними.
Візьмемо для прикладу хоча б ті ж самі поняття, які ми вже приводили: "голонасінні дерева" та "хвойні дерева". Це два різних поняття, оскільки характеризують предмети за різними ознаками. Але означають вони одні і ті ж предмети. Відношення між такого типу предметами за допомогою кругів Ейлера відображається наступним чином:
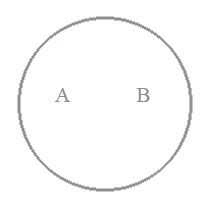
Мал. 2.
Ще одне відношення сумісності – це відношення перетину. Це таке відношення між двома поняттями, коли їх об'єми частково співпадають, але кожне з них має елементи, які не входять до об'єму іншого.
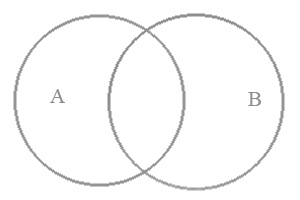
Мал. 3.
Прикладом може служити відношення між поняттями "закон" та "нормативний акт". Деякі закони (юридичні) є правовими актами. Відповідно, деякі правові акти є законами. Але не кожний нормативний акт є законом (є підзаконні акти, інструкції, тощо). Точно так же не кожний закон є нормативним актом (скажімо, закони природи, чи закони логіки).
Відношення несумісності графічно можна виразити двома окремими кругами.
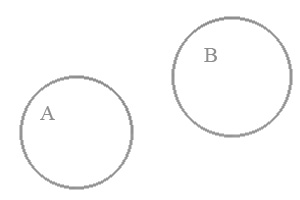
Мал. 4.
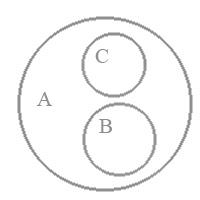
Але можна виділити кілька окремих типів несумісності. Так, практично всі несумісні поняття, за винятком, хіба що категорій, можна представити як супідрядні (співпідпорядковані) поняття. Супідрядними називають такі два несумісних поняття, об'єми яких повністю входять до об'єму третього поняття
Мал. 5.
В такому відношенні будуть перебувати, наприклад, поняття: студент, студент-заочник і студент стаціонару. Неважко помітити, що крім зазначених, до поняття А будуть входити інші поняття. В даному випадку це будуть поняття "студент-вечірник" та "студент дистанційної форми навчання".
Серед супідрядних понять можна виділити ще два окремих типи відношень: відношення протилежності та відношеня суперечності.
Суперечливими називаються два таких поняття, які заперечують один одного і повністю вичерпують об'єм родового поняття.
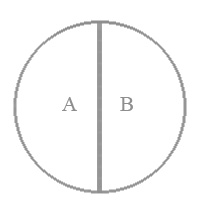
Наприклад, смерть і безсмертя. Найпростішим способом утворення суперечливих понятть є додавання частки не, чи іншої заперечної частки, до позитивного поняття (білий – небілий; студент – нестудент). Хоча, можливі і суперечливі поняття, утворені іншим шляхом. Наприклад, чоловік – жінка, матерія – свідомість. Виділяють ще одне відношення супідрядності - протилежність. Формальна відмінність його від суперечності полягає в тому, що в цьому випадку поняття, які одне одного заперечують, не вичерпують родового поняття.
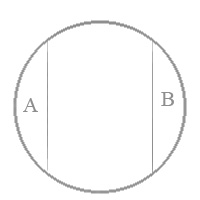
Мал. 7.
Арістотель розглядає відношення суперечності та протилежності між поняттями як два різних види протилежності. Поняття, з яких одне є простим запереченням іншого, знаходяться, на його думку, в відношенні суперечливої протилежності, а поняття, які належать до одного і того ж роду і найбільш відмінні одне від одного, знаходяться в відношенні противної протилежності.
Утворення понять
В формальній логіці вважається, що поняття утворюються через застосування певних логічних операцій. Серед них виділяють операції узагальнення і обмеження, аналізу, синтезу, порівняння, поділу, визначення і т.п. Ми розберемо тільки узагальнення, обмеження, визначення та поділ, оскільки для інших операцій в формальній логіці не розроблені певні процедури і правила, і тому вони не можуть бути з повним правом визнані формально-логічними операціями.
Що стосується операцій узагальнення та обмеження, то ми з ними уже фактично познайомились, коли розбирали відношення підпорядкування ж поняттями. Залаишилось тівльки дати визначення цих операцій. Узагальнення – це логічна операція, за допомогою якої ми шляхом вилучення ознак видової відмінності у видових понять одержуємо родові поняття.
Візьмемо, наприклад, поняття "студент". Вилучимо ознаку "навчатися в вузі" – одержимо поняття "людина". А тепер, навпаки, до поняття "студент" додамо ще одну ознаку "навчатися на факультеті права". Одержимо поняття "студент факультету права". Це ми провели операцію обмеження.
Обмеження – операція, яка дозволяє нам шляхом додавання нових ознак до відомих понять одержувати нові поняття, які будуть підпорядкованих до початкових.
Проаналізувавши ці дві операції досить легко побачити, що між об'ємом та змістом понять існує залежність. Чим багатший зміст поняття (чим більше ознак в ньому мисляться), тим вужчий його об'єм. І навпаки, чим бідніший зміст понять, тим ширший його об'єм.
Велике значення для науки й повсякденного життя має така операція, як визначення понять. Без визначень ми не змогли б сформулювати будь-яких понять і головне, не могли б узгодити своїх понять з поняттями інших людей.
За допомогою визначення розкривається зміст поняття.
Будь-яке визначення складається з двох частин: з того поняття, яке треба визначити, і того, за допомогою якого визначають невідоме поняття.
Візьмемо будь-яке визначення. Наприклад: "логіка – наука про закони та форми мислення".
Тут ясно видно, що воно складається з двох понять: "логіка" – те поняття, яке треба визначити, та "наука про закони та форми мислення" – поняття, за допомогою якого ми визначаємо поняття "логіка". Також очевидно, що операція визначення в даному випадку складалася з двох інших операцій:
1. Операція узагальнення. Ми вказували на те, що логіка відноситься до роду "наука".
2. Операція обмеження. Ми вказували, чим логіка відрізняється від всіх інших предметів цього роду, тобто від інших наук. для цього ми вичленяли дві ознаки. Перша полягала в тому, що логіка є наукою про мислення. Друга – в тому, що логіка вивчає тільки його закони та форми, не торкаючись змісту.
Такого роду визначення називаються визначеннями через рід та видову відмінність.
Вирізняють також генетичні визначення. Генетичними називаються визначення, в яких зміст поняття розкривається шляхом вказування на спосіб утворення предмета чи на його походження. Наприклад, куля – геометрична фігура, яка утворюється шляхом обертання круга навколо одного із своїх діаметрів. Визначення поділяють також на реальні та номінальні.
Реальними називають визначення, в яких зміст поняття розкривається, через розкриття ознак предмета, який виражається в понятті. Як неважко помітити, приведені вище визначення були реальними.
Номінальними (від лат. nominus – ім'я) називають визначення, в якій зміст поняття розкривається, через його назву. Наприклад, візьмемо наступне визначення: Борисфен – давньогрецька назва Дніпра. Можливо, хтось не знав, що означає поняття Борисфен. Але досить було вказати український відповідник цього слова і вже нема ніякої потреби розкривати, що собою являє предмет, який позначався словом Борисфен.
Виділяють явні та неявні визначення. Явними називають ті визначення, в яких зміст поняття розкривається через розкриття ознак позначеного в понятті предмета. Всі приведені вище визначення були явними. Але бувають випадки, коли ми не маємо змоги вияснити ознаки предмета, який нас цікавить, але знаємо ознаки інших предметів, які з ним певним чином пов'язані. Наприклад, коли були відкриті віруси, вони були визначені як "мікроорганізми, які фільтруються" (по-російськи: фильтрущиеся микроорганизмы). Ніякі ознаки нововідкритих форм життя не були відомі, крім тої, що вони здатні викликати хворобу тютюнової мозаїки і в той же час вони проходили через керамічні фільтри з настільки малими порами, що через них не могли пройти навіть найменші бактерії.
Визначення, які розкривають зміст поняття через ознаки інших предметів, з ним пов'язаних, називаються неявними.
Головні вимоги, які висуває формальна логіка до визначення – це ясність, точність, а також співмірність того поняття, яке визначається, з тим, за допомогою якого здійснюється визначення.
Вимога співмірності полягає в тому, що об'єм поняття, яке визначається і об'єм поняття, за допомогою якого визначають, мають знаходитися в відношенні тотожності. Якщо об'єм поняття, за допомогою якого визначають, буде більшим, за об'єм поняття, яке визначають, таке визначення називають широким. Якщо меншим – вузьким. Наприклад, визначення "сосна – це дерево" буде широким. Визначення "авіація – це повітряні транспортні засоби для перевезення пасажирів" буде, навпаки вузьким, тому що авіація виконує ще й багато інших завдань. Визначення має бути ясним. Це означає, що воно має бути зрозумілим. Не можна визначати незрозуміле через ще більш незрозуміле. Або ж через нього самого.
Помилки, які виникають внаслідок порушення цієї вимоги називаються помилками "неясного визначення". Один із видів такого роду помилок – "тавтологія".
Наприклад, в одному із відомих словників читаємо "протилежність – предмет чи явище, які протилежні іншим…"
Іншим видом неясного визначення буде „коло в визначенні”. В цьому випадку той факт, що поняття визначається через нього ж самого, виявляється не зразу, а згодом. Дуже гарний приклад приводиться в відомому підручнику з логіки проф. Г. І. Челпанова: „Візьмімо, наприклад, визначення „обертання є рух навколо осі”. Це визначення поняття „обертання” через поняттяя вісь робить коло, бо саме поняття „вісь” визначається тільки через поняття „обертання” (як відомо, вісь, це пряма, навколо якої відбувається обертання”.
Визначення має бути точним, тобто однозначним. Це означає, що в визначеннях не можна вживати метафор і інших понять, які можна розуміти двояко.
Небажано давати негативні визначення за виключенням тих випадків, коли поняття не може бути визначене іншим способом. Наприклад, неможливо визначити, що таке нескінченність інакше, як через заперечення кінечного.
Бажано, щоб всі визначення задовольняли приведеним вище вимогам. Але не завжди цього можна досягти навіть в науці. Тому часто доводиться використувати операціями, які не у всьому відповідають правилам визначення, але більш чи менш повно заміняють визначення.
Назвемо ці операції псевдовизначеннями.
Серед них найбільш розповсюджені: безпосередня вказівка, опис, характеристика, порівняння, розрізнення. Безпосередня вказівка застосовується як правило тоді, коли ми маємо визначити найпростіші поняття, як от: „лазуровий колір”, „високий звук”, „низький звук” і т. п. Дати таким поняттям визначення практично неможливо, та й нема потреби, значнол легше й дохідливіше безпосередньо вказати на них тому, хто не розуміє, що це таке.
Опис грає дуже велику роль при першому ознайомленні з предметами, особливо в випадках, коли важливу роль грають їх індивідуальні особливості, а не загальні якості. Коли біолог відкриває новий вид рослин чи тварин, хімік – нову сполуку, геолог – нове родовище, вони обов’язково виконають докладний опис, оскільки формально правильного визначення нововідкритого буде недостатньо, щоб скласти про нього правильне уявлення.
Неможливо обійтись без детальних описів в криміналістиці, в військовій справі, не кажучи вже про художню літературу.
Згадайте, що вийшло, коли у відомій повісті Драгунського про Дениса Корабльова вчителька географії попробувала замінити художній опис української ночі у Пушкінській „Полтаві” сукупністю наукових визначень: „- Нет, - сказала Елизавета Николаевна. - Пойми же ты, что в словах "Тиха украинская ночь" удивительно тонко подмечено, что Украина находится в стороне от центра перемещения континентальных масс воздуха. - "Прозрачно небо". ... В этих двух, как бы ничего не значащих словах Пушкин рассказал нам, что количество выпадающих осадков в этом районе весьма незначительно, благодаря чему мы и можем наблюдать безоблачное небо. Теперь ты понимаешь, какова сила пушкинского таланта? Давай дальше.
Но мне уже почему-то не хотелось читать. Как-то все сразу надоело”.
Характеристика на відміну від визначення, наводить не істотні ознаки, а особливо прикметні для цього предмета. Іноді знання цих прикметних ознак значно важливіше як знання істотних ознак. Наприклад, при розшуку якоїсь людини приводять характерні ознаки. Скажімо, вказують на звичку гризти нігті. Звичайно, така ознака не є істотною для будь-якої людини, але вона може допомогти в ідентифікації особи деколи не гірше як фотографія. За фотографією не так уже легко вичленити людину серед великої кількості інших людей, а звичка гризти нігті зразу зверне на себе увагу.
Порівняння – це логічний прийом, за допомогою якого ми встановлюємо різницю між предметами, чи знаходимо подібні ознаки. Як правило, порівняння не може замінити визначення, але будь-яке визначення не може обійтися без попереднього порівняння предмета, який нас цікавить, з іншими предметами. Першим ступенем визначення поняття через рід та видову відмінність буде віднесення предмету поняття, яке визначається, до найближчого роду, а це неможливо зробити, не порівнявши цей предмет з іншими і не знайшовши спільних ознак.
Так само неможливо без порівняння визначити видову відмінність.
Важливе значення має операція поділу понять.
Поділ – це операція, за допомогою якої розкривається об'єм понять. Будь-який поділ відбувається за певною ознакою, яку називають основою поділу.
Розрізняють два види поділу: дихотомію та поділ за видозміною основи.
Дихотомія – це поділ поняття на два суперечливих, коли одне з них є запереченням іншого.
Наприклад, в результаті застосування дихотомії до поняття "природа" ми одержимо поняття "жива природа" і "нежива природа".
Основою дихотомії виступає наявність або відсутність ознаки у предмета.
Поділ за видозміною основи, чи, інакше, класифікація – це поділ понять на підкласи залежно від ознаки, яка вибрана за основу поділу.
Наприклад, поняття "людина" ми можемо поділити багатьма способами.
За статтю – на чоловіків та жінок.
За расами – європеоїди, монголоїди, негроїди і т. д.
Можна ділити за національністю, можна за рівнем освіти, можна навіть за розміром взуття
.Може здатися, що останній поділ буде недоречним, що він буде відбуватися за несуттєвою ознакою. Насправді це не так. Суттєвість чи несуттєвість ознаки залежить від обставин і від мети, з якою ми будемо здійснювати поділ. Коли мова буде йти, скажімо, про військових інтендантів, то для них не важливо, як військовослужбовці їх частин діляться за расами чи національностями, але дуже важливо, як вони діляться саме за розміром взуття та одягу.
До поділу в логіці теж пред'являються певні вимоги.
Так, поділ, як і визначення має бути співмірним. Правда, на відміну від визначення, куди входить завжди тільки два поняття, він буде складатися з трьох і більше понять. Поняття, яке ділиться, називається діленим. Ті поняття, які одержуються в результаті поділу, називаються членами поділу. Вимога співмірності полягає в тому, що сума об'ємів членів поділу має бути рівною об'єму діленого поняття.
Наприклад поділ поняття "гілки влади" на "законодавча влада", та "виконавча влада" буде неправильним, тому що він неповний. Не врахована судова гілка влади.
Поділ мусить здійснюватися тільки за одною основою. Не можна ділити поняття за двома ознаками одночасно. Наприклад, неправильно буде ділити людей, наприклад, на робітників, селян, інтелігенцію та інвалідів. При порушенні цього правила виникає помилка, коли члени поділу перекривають один одного. В нашому випадку, частина робітників, селян, інтелігентів виявиться інвалідами.
Але не буде помилкою, коли після поділу поняття за одною основою, ми поділимо один з одержаних підкласів за якоюсь іншою основою, тобто, коли ми будемо виконувати операцію підрозділ. Наприклад, не можна ділити людей на французів, німців, англійців, мусульман та християн, оскільки тут переплутані дві різні ознаки поділу – за національністю і за релігійною приналежністю, але нічого не заважає нам поділити німців чи французів на християн, мусульман, іудаїстів і т. д.
Поділ має бути безперервним.
Це означає, що об’єм поняття треба ділити на найближчі роди.
Наприклад, виділяють спочатку царства живої природи: тварини, рослини, гриби, віруси, бактерії, пріони. Царства тварин та рослин діляться на підцарства: одноклітинних та багатоклітинних. Підцарства поділяться на типи. Для тварин це: хордові, членистоногі, найпростіші, губки, плоскі черви, круглі черви, молюски і т. д. Типи діляться на класи. Для хордових це: риби, земноводні, рептилії, птахи та ссавці.
А от тип членистоногих включає в себе чотири підтипи, в одному з яких виділяють чотири класи, а в іншому – три, але один з цих класів має десять рядів.
Погодьтеся, що будь-яка спроба поділити, хоча би тварин, зразу на класи, чи, більше того, на ряди, привела б тільки до плутанини.
Дотримання правила безперервності поділу має не тільки пізнавальне значення.
Управління більш чи менш складними системами (як технічними, так інформаційними, а також адміністративними і громадськими) неможливе без ієрархії. А в основі ієрархії лежить саме послідовний поділ. Наскільки вдало нам вдасться визначити „поверхи” управлінських структур, настільки ефективною виявиться, в кінці кінців, вся система управління в цілому.