Тема 5. Судження.
Загальна характеристика та структура судження.
В формальній логіці судженням називають форму мислення, в якій фіксується відношення між предметами та їх ознаками. Будь-який предмет і будь-яка ознака можуть бути пов'язані між собою двояко: або в предмета якась ознака є, або цієї ознаки в цього предмета нема.
Просте категоричне судження (тобто таке судженя, в якому стверджується або заперечується навність ознаки у предмета) складається з двох термінів. Термінами називаються поняття, які входять до складу судження. Термін, який позначає предмет, називається суб'єктом. Термін, в якому виражається ознака предмета, називається предикатом. Терміни поєднуються між собою зв'язками "є" або "не є". Також до складу судження входять квантори – слова, або знаки, які вказують на те, чи є судження загальним (квантор "всі"), чи частковим (квантор "деякі"). Треба звернути особливу увагу на те, що більше ніяких частин в складі простого судження бути не може.
Не всі частини судження виступають явно в граматичній формі. Візьмемо судження "Всі люди смертні". Тут неважко визначити суб'єкт - "люди", предикат – "смертні", квантор – "всі". А от зв'язка "є" тут граматично не виражена. Вона тут існує в неявному вигляді. Така специфіка української (точно так же як і російської) мови, що в них присудок, виражений дієсловом "є" може опускатися.
Таким чином, загальна структура будь-якого просто категоричного судження може бути виражена в формулах:
S є Р, або S не є Р
Класифікація суджень.
За складом всі судження можна поділити на прості та складні.
Простими ми будемо називати такі судження, до складу яких входить один суб”єкт і один предикат. Складними вважаються судження, які включають в себе два або більше простих суджень, поєднаних між собою логічними сполучниками.
Часто судження поділяють за модальністю на три різні групи: ймовірні (проблематичні), достовірні (асерторичні) та судження необхідності (аподиктичні).
До ймовірних відносять судження, в яких та чи інша ознака стверджується чи заперечується у предмета тільки з певною мірою здогадки. Формула судження ймовірності: „S, можливо, є Р”.
Достовірними називають судження, відносно яких цілком відомо, що та чи інша ознака притаманні або не притаманна даному предмету. Формула цього судження: „S є Р”.
Судженнями необхідності виражають такий зв’язок між предметом та ознакою, який буде дійсним за будь-яких обставин. В судженнях необхідності виражаються, як правило, закони, аксіоми, постулати та положення, які з них витікають.
Розрізняють також категоричні судження, в яких йдеться про приналежність ознаки предмету чи відсутність ознаки у предмета та судження з відношеннями.
За якістю всі прості категоричні судження можуть бути поділені на два великих класи, залежно від того, йдеться в них про наявність ознаки у предмета, чи наявність цієї ознаки у предмета заперечується. Судження, в яких стверджується наявність ознаки у предмета називають стверджуючими.
Судження, в яких говориться про те що якийсь предмет не має цієї ознаки, називають заперечними. За кількістю прості категоричні судження поділяються на загальні (коли ознака належить всім предметам даного класу) та часткові (коли ознака належить тільки частині предметів класу).
Тобто загальні судження можна поділити на стверджувальні та заперечні в, відповідно, так же можна поділити часткові. Точно так же, стверджувальні діляться на часткові та загальні, як і заперечні.
Будь-яким із цих способів ми можемо одержати класифікацію, яка носить назву об'єднаної класифікації простих категоричних суджень за кількістю та якістю.
Об'єднана класифікація простих категоричних суджень дає поділ їх на чотири класи: Загальностверджувальні, які мають структуру – всі S є Р; частковостверджувальні – І – деякі S є Р; загальнозаперечні – Е – всі S не є Р (інколи судження цього типу формулюють так: ні один S не є Р, або жоден S не є Р; частковозаперечні – О – деякі S є Р. кожне з них прийнято в логіці позначати певними буквами: загальностверджувальні – А; загальнозаперечні – Е; частковостверджувальні – І; частковозаперечні – О
Відношення між простими категоричними судженнями за істинністю.
Поділивши всі прості категоричні судження за кількістю та якістю, ми одержуємо можливість чисто формально, не знаючи змісту суджень встановлювати їх істинність чи хибність, виходячи тільки із знання про значення суджень іншого типу.
Припустимо, що судження типу А, тобто загальностверджувальне судження (всі S є Р), є істинним. Неважко зробити висновок, що частковостверджувальне судження І (деякі S є Р) в цьому випадку теж буде істинним, оскільки, якщо всі предмети класу S мають ознаку Р, то деякі предмети цього класу теж мусять мати цю ознаку.
Загальнозаперечне судження Е (всі S не є Р) буде хибним. Це теж очевидно: якщо нам відомо, що істинним буде судження типу А (всі S є Р), то судження Е (всі S не є Р) мусить бути хибним, оскільки одночасно істинними вони не можуть бути.
Хибним буде також і частковозаперечне судження О (деякі S не є Р). Адже нам відомо що всі S мають ознаку Р, значить, що судження „деякі S не мають ознаки Р” не може відповідати дійсності.
Таким чином, ми одержуємо три співвідношення:
Аі – Іі Аі – Ех Аі – Ох
Тепер істинним будемо вважати загальнозаперечне судженя Е (всі S не є Р). Зрозуміло, що за цієї умови істинним буде також і частковозаперечне судження О (деякі S не є Р), якщо ні один предмет класу S не має ознаки Р, то не можуть мати цієї ознаки і деякі предмети цього класу. Отже судження „деякі S не є Р” буде відповідати дійсності, тобто буде істинним. Судження А (всі S є Р) за умови істинності загальнозаперечного судження буде, звичайно, хибним. Хибним також буде і частковостверджувальне судження. Бо якщо нам відомо, що жодне S не має ознаки Р, то судження „деякі S є Р” ніяк не може бути істинним.
Отже, якщо нам відомо, що загальнозаперечне судження істинне, то ми можемо записати: Еі – Оі Еі – Ах Еі – Іх
Тепер будемо вважати істинним судження типу І (деякі S є Р). За цієї умови очевидно, що хибним буде судження типу Е (всі S не є Р). Що стосується загальностверджувального судження А (всі S є Р), то про нього ми не можемо сказати, чи буде во но істинним, чи хибним, оскільки нам відомо тільки те, що частина класу S має ознаку Р. Інша частина може теж мати ці ознаки, і тоді судження А було б істинним, але може і не мати – тоді загальностверджувальне судження буде хибним. Отже, коли нам відомо, що частковостверджувальне судження істинне, то загальностверджувальне залишається невизначеним, оскільки даної нам в частковостверджувальному судженні інформації про приналежність ознаки Р класу предметів S недостатньо для того, щоб стверджувати чи заперечувати істинність загальностверджувального судження. Невизначеним в цьому випадку буде також і частковозаперечне судження, знаючи тільки те, що деякі предмети класу S мають ознаку Р, ми ще нічого не можемо сказати з приводу того, чи мають, чи не мають цю ознаку інші предмети цього класу.
Іі – Ех Іі – Ан Іі – Он
Візьмемо за істинне частковозаперечне судження О (деякі S не є Р). Це буде означати, що загальностверджувальне судження А (всі S є Р) буде хибним. Загальнозаперечне Е (всі S не є Р) буде в цьму випадку невизначеним з тих же причин, які були вказані для відношення Іі – Ан. Невизначеним буде також за даної умови і частковостверджувальне судження І (деякі S є Р) з тих же причин,з яких істингність частковостверджувального судження І зумовлювала невизначеність частковозаперечного О.
Отже: Оі – Ах Оі – Ен Оі – Ін
Але це ще не всі відношення, які ми можемо встановити між простими категоричними судженнями за їх істинністю чи хибністю.
Ми ще можемо припустити, що судження типу А (всі S є Р) є хибним. Звідси однозначно можна вивести, що істинним буде частковозаперечне судження О (деякі S не є Р). Адже А (всі S є Р) буде хибним тоді і тільки тоді, коли, як мінімум, деякі предмети класу S не матимуть ознаки Р, що і фіксується в частковозаперечному судженні. В той же час хибність загальностверджувального судження не зумовлює хибності судження частковостверджувального. Судження типу І (деякі S є Р) за умови хибності судження А (всі S є Р) може бути як хибним, так і істинним. Візьмемо приклад. Скажімо, нам відомо, що неправда, що всі студенти якої-небудь групи здали екзамен з логіки на „5”. Звичайно, що цієї інформації неможливо вивести: істинним, чи хибним буде судження „деякі студенти цієї групи здали логіку на „5””. На перший погляд може здатися, що хибність загальностверджувального судження А (всі S є Р) зумовить істинність загальнозаперечного судження Е (всі S є Р). Насправді це не так. Загальнозаперечне судження в цьому випадку буде невизначеним. Адже загальностверджувальне судження А (всі S є Р) може бути хибним з двох різних причин. Одна з них – коли Е (всі S є Р) – істинне. Але судження А буде хибним і тоді, коли істинним буде тільки частковостверджувальне судження О, тобто, коли тільки деякі S не матимуть ознаки Р. Загальнозаперечне судження в цьому випадку цілком може бути теж хибним.
Ах– Оі Ах– Ін Ах– Ен
Коли хибним ми вважитимемо судження типу Е (всі S не є Р), то істинним буде частковостверджувальне судження. Це очевидно: якщо неправда, що деякі S не мають ознаки Р, це може означати тільки одне – що деякі S мають ознаку Р. Частковозаперечне судження буде невизначеним, оскільки невідомо, з якої саме причини Е буде хибним – чи тому, що насправді всі S мають ознаку Р, чи тому, що тільки деякі її мають, а деякі все-таки не мають. Невизначеним буде також і загальностверджувальне судження з тих же причин, з яких хибність Судження типу А зумовлювала невизначеність суджень типу Е.
Ех – Іі Ех – Он Ех – Ан
Тепер припустимо, що хибним є частковостверджувальне судження І (деякі S є Р). Зрозуміло, що якщо неправда, що деякі предмети класу S мають ознаку Р, то судження А (всі S є Р) і подавно буде хибним. Зате загальнозаперечне судження в випадку хибності частковостверджувального буде однозначно істинного. Адже якщо неправда, що деякі S мають ознаку Р, це може значити тільки одне – що жоден предмет класу S цієї ознаки не має. Частковозаперечне судження О (деякі S не є Р) за умови хибності частковостверджувального теж буде істинним. Неможливо припустити, щоб одночасно хибними були судження „деякі S є Р” і „деякі S не є Р”. Одне з таких суджень мусить бути істинним. Візьмім для прикладу два часткових судження: „деякі люди мають вищу освіту” і „деякі люди не мають вищої освіти”. Звичайно, обидва цих судження можуть бути одночасно істинними. А але неможливо уявити, як би вони могли бути одночасно хибними. Звичайно, що якщо одне з таких суджень буде хибним, то інше, обов’язково мусить бути істинним.
Іх – Ах Іх – Еі Іх – Оі
Залишилось взяти ще одне припущення: що судження типу О (деякі S не є Р) хибне. Навіть не задумуючись по суті питання, а діючи за аналогією до того, як ми діяли, припускаючи хибність частковостверджувального судження, ми одержимо, що в випадку хибності частковозаперечного судження О (деякі S не є Р) хибним буде також і судження Е (всі S не є Р). Аналогія легко підтверджується міркуванням: якщо неправда, що навіть деякі предмети класу S не мають ознаки Р, то очевидно, що неправдою буде і те, що всі предмети класу S не мають ознаки Р. Але це означає, що всі предмети класу S мають ознаку Р. І дійсно, якщо судження типу О (деякі S не є Р) хибне, тоді судження типу А (всі S є Р) вочевидь буде істинним. Відношення між судженнями типу О (деякі S не є Р) і типу І (деякі S є Р) вже розібрані вище.
Таким чином, ми одержали останню групу можливих відношень між простими категоричними судженнями за істинністю:
Ох – Ех
Ох – Аі
Ох – Іі
Неважко помітити, що в відношеннях між різними типами суджень існує певний алгоритм. Так, скажімо, відношення між загальнозаперечними судженнями та частковозаперечними будуть подібні до відношень між загальностверджувальними та частковостверджувальними судженнями. Істинність загальних суджень визначає істинність часткових суджень тої ж якості, а хибність часткових суджень зумовлює хибність загальних тої ж якості. Таке відношення називається відношенням підпорядкування.
Можна згрупувати певним чином і інші відношення між судженнями. Для наочності в розумінні різних типів відношень між судженнями та для полегшеня запам’ятовування в логіці традиційно використвується так званий логічний квадрат. Букви на вершинах означають чотири основні типи суджень.
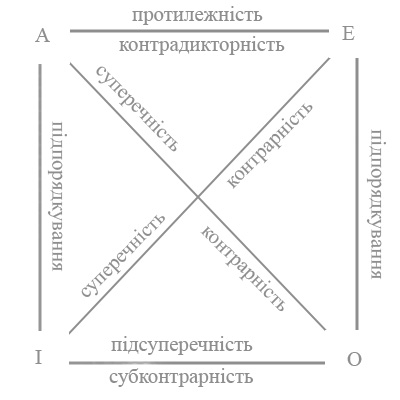
Мал. 8.
Отже, вертикальні сторони квадрата будуть символізувати відношення підпорядкування між судженнями. Відношення по діагоналях (між загальними судженнями та частковими судженнями протилежної якості) будуть називатися відношеннями суперечності або контрарності. Суть його в тім, що судження, які знаходяться в відношенні суперечності повністю одне одного виключають. Якщо одне з них істинне, то інше обов’язково хибне і навпаки – якщо одне хибне, то інше обов’язково істинне. Наприклад, якщо істинне загальностверджувальне судження А „всі люди смертні”, то суперечливе до нього судженя типу О „деякі люди не є смертними” однозначно буде хибним. Коли ми візьмемо якесь істинне частковозаперечне судження:, скажімо „деякі люди не вміють грати в шахи”, то загальностверджувальне судження А „всі люди вміють грати в шахи” беде очевидно хибним.
Відношеня протилежності, тобто відношення між загально стверджувальними А та загальнозаперечними Е судженнями (воно символізується верхньою стороною логічного квадрата) відрізняється від відношення суперечності тим, що істинність одного з таких суджень точно так же визначає хибність іншого, а ле хибність одного ще не значає істинності іншого. Судження А і Е можуть бути одночасно хибними.
Відношення по нижній стороні квадрата (між частковими судженнями різної якості) називається відношенням підсуперечності або субконтрарності. Його суть в тому, що два часткових судження, які перебувають в цьому відношені, можуть бути одночасно істинним, але не можуть бути одночасно хибними.
Розподіленість термінів в простих категоричних судженнях
Розподіленими називаються ті терміни, які взяті в судженні в повному об'ємі, тобто об'єм яких повністю включається до об'єму іншого терміну цього судження, або повністю з нього виключається. Відповідно, нерозподіленими будуть ті терміни, об'єм яких частково включається в об'єм іншого терміна, або частково з нього виключається.
За допомогою кругів Ейлера ми маємо змогу прослідкувати, яким чином співвідносяться між собою терміни в судженнях.
В загальностверджувальних судженнях можливі два варіанти співвідношення термінів: 1) Підпорядкування, коли об'єм суб'єкта повністю входить до об'єму предиката:
Мал. 9.
Наприклад, всі громадяни України мають право на працю
2) Тотожності, коли об'єми суб'єкта та предиката співпадають.
Мал. 10.
Наприклад, всі квадрати (S) є прямокутними ромбами (Р).
Таким чином, в загальностверджувальних судженнях суб'єкт завжди розподілений. Це видно не тільки з діаграм, але й з того, що тут є квантор "всі".
Предикат може бути розподіленим – в випадку, коли суб'єкт і предикат знаходяться в відношенні тотожності (мал. 10), а може бути нерозподіленим, коли предикат є підпорядковуючим поняттям по відношенню до суб'єкта (мал. 9).
В загальнозаперечних судження буде тільки один варіант співвідношення термінів:
Мал. 11.
Наприклад, людина (S) не може жити поза суспільством (Р).
В судженнях цого типу обидва терміни є розподіленими, оскільки вони є несумісними, тобто повністю виключають один одного.
В частковостверджувальних знову два варіанти: підпорядкування, але коли підпорядкованим буде предикат;
Мал. 12.
Деякі юристи – адвокати
Частковостверджувальні судження такого типу називають інколи виділяючими;
і, звичайно, перетину.
Мал. 13.
деякі юристи – спортсмени
В частковостверджувальних судженнях суб'єкт завжди буде нерозподіленим. Це видно як з діаграм, так і з того, що квантором тут буде слово "деякі", яке саме по собі означає, що суб'єкт береться не в повному об'ємі, а тільки частково.
Предикат може бути розподіленим, коли він буде підпорядкованим поняттям по відношенню до суб'єкта (мал. 12), і нерозподіленим, коли суб'єкт і предикат знаходяться в відношенні перетину (мал. 13)
В частковозаперечних судженнях виразити співвідношення термінів за допомогою кругів Ейлера неможливо. Тут можна використати так звані діаграми Ейлера-Венна, які відрізняються від кругів Ейлера тим, що в них можна позначати не тільки ті області, які належать обом множинам, але й ті, які не належать одній з них, або не належать обом.
Візьмемо приклад:
деякі студенти (S) не є відмінниками (Р).
Зобразимо відношення між термінами цього судження за допомогою діаграми:
мал. 14
Ми одержали відношення перетину.
Тепер візьмемо трохи інакше судження:
деякі ссавці (S) не є плацентарними тваринами (Р)
Це буде відношення підпорядкування.
Тобто ми одержали такі ж відношення між термінами, як і в частковостверджувальних судженнях. Різниця буде в тому, що в частковостверджувальних судженнях ми звертали увагу на ті області об’ємів термінів, які є для них спільними, а в частковозаперечних судженнях нас цікавить те, що в термінах не збігається.
Звичайно, що частина студентів все-таки є відмінниками, але в даному судженні ця частина нас не цікавить. В ньому говориться про тих студентів, які відмінниками не є. Це значить, що кожен відмінник, в тому числі той, який є студентом, виключається з розгляду в даному судженні.
Це ж стосується і другого прикладу. Фактично в цьму прикладі нас цікавлять сумчасті. А ні один сумчатий не належить до плацентарних.
Таким чином, предикат в частковостверджувальних судженнях буде кожен раз розподіленим, тобто буде повністю виключатися з об’єму суб’єкта.
Складні судження
Складними судженнями називають судження, які складаються з двох або більше простих. Прості судження поєднуються між собою за допомогою логічних сполучників кон'юнкції (їй відповідає в мові сполучник і), диз'юнкції (або в сполучно-роз’єднувальному значенні; хоча б одне з двох), строгої диз'юнкції (або в значенні або одне, або інше), імплікації (якщо то), еквіваленції (якщо,і тільки якщо).
Позначимо прості судження, які входять до складу складних, великими буквами латинського алфавіту:
A, B, C, D і т. д. Для позначення логічних сполучників скористаємося спеціальними знаками. Ми будемо використовувати одну із систем цих знаків, але в дужках подаємо й інші, які найчастіше зустрічаються в літературі:
& – кон’юнкція, сполучник „і” ⋁ – диз’юнкція, сполучник „або” ⊽ – строга диз’юнкція (⇒,→) – імплікація, сполучник „якщо, то”. ∼ (≡,↔,⇔) – еквіваленція, „якщо і тільки якщо” – заперечення
Складні судження, утворені за допомогою кон'юнкції, називають поєднувальними, ті, які утворені за допомогою диз’юнкції – розділовими, а судження, утворені за допомогою імплікації та еквіваленції, називаються умовними.
Візьмемо кілька прикладів.
Скажімо, вчителька географії в школі запронувала учням такий тест:
В кожному з рядочків названо по два міста. Вибрати ті рядочки, в яких перше і друге міста є містами Сполучених Штатів Америки:
1. Чикаго, Сіетл;
2. Атланта, Житомир;
3. Воронеж, Пітсбург;
4. Жмеринка, Берлін.
Після цього вчителька запропонувала учням з тих же пар міст вибрати ті, в яких або одне, або інше місто було би містом Сполучених Штатів.
Звичайно, що в першому випадку учні вибрали би тільки першу пару міст, а в двідповіді на друге питання вони підкреслять варіанти 1), 2), 3).
Пари міст залишалися такими ж, але відповіді були різні. Причина в тому, що в питаннях вживалися два різних сполучники: в першому випадку „і”, в другому „або”.
Побудуємо таблички значень логічних сполучників для кожного з цих прикладів:
Для кон’юнкції (сполучник „і”) ці значення будуть такі:
| A | B | A&B |
| і | і | і |
| і | х | х |
| х | і | х |
| х | х | х |
мал.15
Тобто кон’юнктивне складне судження буде істинним тільки в одному випадку – коли обидва простих судження, які входять до його складу, будуть істинним. В нашому прикладі це значило, що і одне місто, і інше мали бути містами США. Тому правильна була відповідь тільки за першим варіантом: Чікаго, Сіетл. Всі інші варіанти цій вимозі не відповідали, отже були хибними.
Зовсім інша річ виходить, коли питання було сформульоване за допомогою сполучника „або”. Тепер правильними будуть будь-які варіанти відповідей, за винятком одного – четвертого, в якому названі міста, ні одне з яких не є містом США.
| А | В | AνB |
| і | і | і |
| і | х | і |
| х | і | і |
| х | х | х |
Мал. 16
Таким чином, розділове судження в нашому прикладі виявляється істинним, якщо хоча б одна з альтернатив (частини розділового судження називаються альтернативами) буде істинною. Відповідно, хибним буде тільки те диз’єюнктивне судження, в якому всі альтернативи хибні.
Але це стосується тільки одного типу диз’юнктивних суджень. А сполучник „або” має не одне, а два значення.
Візьмемо два приклади:
- Марії подобається Іван або Степан.
- Марія виходить заміж за Івана або за Степана.
В цих на перший погляд подібних судженнях значення сполучника або будуть суттєво відрізнятися. Марії цілком може подобатися як Іван, так Степан, так і обидва одночасно. А от виходити заміж вона може тільки за одного з них.
В першому прикладі ми маємо справу зі звичайною диз’юнкцією. Сполучник „або” тут має поєднувально-розділове значення. Розділове судження утворене за допомогою звичайної диз’юнкції буде істинним в будь-якому випадку, крім того, коли обидві альтернативи хибні (див. таблицю на мал. 16).
В другому прикладі, в якому мова йшла про заміжжя, сполучник „або” має строго розділове значення. Складне судження, утворене за допомогою такого сполучника, буде істинним тільки тоді, коли альтернативи, які входять до його складу, будуть мати різне значення. Якщо обидві альтернативи істинні, то розділове судженя, утворене за допомогою строгої диз’юнкції, буде хибним
| А | В | A⊽B |
| і | і | х |
| і | х | і |
| х | і | і |
| х | х | х |
Мал. 17
Умовне (імплікативне) судження виражає зв’язок між причиною та наслідком. Та частина умовного судження, в якій йдеться про причину, називається основою або антецедентом. Судження, яке виражає наслідок, що витікає з вказаної в судженні причини, називається консеквентом, або ж просто наслідком.
Якщо і основа і наслідок умовного судження істинні, то таке судження теж буде істинним. Якщо основа істинная, а наслідок хибним, то таке умовне судження буде хибним, бо з істини має випливати істина. Якщо і основа і наслідок хибні, то таке умовне судження буде істинним, оскільки з хиби і має випливати хиба. Дуже цікавим є випадок, коли основа імплікативного судження хибна, а наслідок істинний. Якщо підійти формально, то таке судження має бути визнаним хибним, адже з хиби має слідувати хиба, а тут з хиби слідує істина. Некоректним є таке судженя і з точки зору закону виключеного третього: не можуть бути одночасно істинними два судження, якщо в одному з них із хиби випливає хиба, а в іншому – істина. Але, не зважаючи на все це, умовне судження, в якомцу основа хибна, а наслідок істинний, все ж вважається істинним. Формальна логіка в цьому випадку змушена визнати, що дійсним критерієм істинності чи хибності суджень є тільки практика. На практиці ж люди, одержавши істинний висновок, не зважають на те, чи були істинними ті судження, з яких він випливає. Дуже показовим в цьому плані є історія з винайденням повітряної кулі. Її винахідники, брати Монгольф’є, за переказом, мислили наступним чином:
-- Духи, -- говорили вони, -- легші за повітря, оскільки завжди піднімаються вгору. Якщо наповнити духами зшиту з непроникної для газів матерії кулю, то при певному співвідношенні об’єму кулі, та їїмаси разом з вантажем, вона має піднятися в повітря. „Рослинні духи” брати добували шляхом спалювання соломи, а „тваринні духи” – спалюючи кізяки. Наповнивши цими „духами” кулю, вони добилися того, що вона полетіла. Через певний час людство здогадалося, що в міркуваннях братів була помилка. Що насправді куля наповнювалася не духами, а теплим повітрям, яке, як відомо, легше за повітря холодне. Але, погодьтеся, було б дивно якби люди на цій основі відмровилися від користування повітряною кулею.
Неважливо, з яких основ ми одержали правильний висновок, важливо, що результат істинний.
| А | В | A→B |
| і | і | і |
| і | х | х |
| х | і | і |
| х | х | і |
Мал. 18
Судження, утворене за допомогою еквіваленції відрізняється від імплікативного тим, що коли його основа хибна, а наслідок істинний, то судження теж вважається хибним. Це зумовлено тим, що в еквівалентному судженні не тільки наслідок випливає з основи, а й навпаки, основа має випливати зі свого власного наслідку. Наприклад: якщо ця фігура є прямокутним ромбом, то це квадрат. Звичайно, що таке судження можна повернути наступним чином: якщо ця фігура – квадрат, то вона є прямокутним ромбом.
Зверніть увагу, що в випадку імплікації цього зробити не можна. Наприклад. Якщо йде дощ, то асфальт мокрий. Ми ніяк не мрожемо сказати: якщо асфальт мокрий, то йде дощ. Адже асфальт може бути мокрий з інших причин.
| А | В | A↔B |
| і | і | і |
| і | х | x |
| х | і | x |
| х | х | і |
Мал. 19
Зведемо всі розглянуті значення логічних сполучників в одну довідкову таблицю.
Мал. 19
Зведемо всі розглянуті значення логічних сполучників в одну довідкову таблицю.
| А | В | A&B | AνB | AνB | AνB | AνB |
| і | і | і | і | х | і | і |
| і | x | х | і | і | х | х |
| x | і | х | і | і | х | х |
| x | x | х | х | х | і | і |
Мал. 20
За допомогою табличної побудови логіки висловлювань, навіть не знаючи змісту суджень, можна визначати, чи є те чи інше судження логічним законом, тобто, чи буде воно істинним, чи хибним. Якщо те, чи інше судження є логічним законом, це означає, що воно буде істинним, незалежно від того, який зміст потім ми вкладемо в цю формулу. Така властивість складних суджень дозволила покласти їх в основу комп’ютенрного програмування.
Візьмемо приклад складного судження і попробуємо за допомогою таблиці визначити, чи буде воно логічним законом:
(AÉB) ν ¬(С&D)
Для того, щоб визначити, чи є це судженя логічним законом, побудуємо таблицю. Буквами у нас прозначені прості судження. Ми не знаємо змісту простих суджень, які входять до складу нашої формули, але із закону виключеного третього нам відомо, що будь-яке судження в рамках традиційної логіки може мати тільки два значення – істина або хиба. В перших двох стовпчиках переберемо всі можливі варіанти поєднання значень простих суджень. Можливі варіанти: коли обидва судження істинні, коли судження А істинне, а В – хибне, навпаки, А хибне, В – істинне, і коли оба судження хибні. Перебір можливих варіантів поєднання значень суджень для кожної нової пари суджень повинен здійснюватися в тому ж самому порядку, який ви вибрали в першому випадку. Далі будемо здійснювати дії аналогічно тому, як це робиться в арифметиці, – спочатку дія в дужках, потім – дія між дужками. Значення сполучників будемо брати з довідкової таблиці. Результати дій в дужках для зручності будемо позначати арабськими цифрами.
| A | B | AÉB | C | D | С&D | ¬(С&D) | 1ν2 |
| і | і | і | і | і | і | х | і |
| і | х | х | і | х | х | і | і |
| x | і | і | х | і | х | і | і |
| х | х | і | х | х | х | і | і |
В останньому стовпчику ми отримали істинні значення в усіх рядочках.
Треба зауважити, що викладений метод визначення істинності складних суджень є недосконалим. Він є дуже зручним, але не дає стопроцентного результату. Ним можна користуватися тільки для пропереднього аналізу складних суджень. Для того, щоб точно визначити, чи є те чи інше складне судження логічним законом, потрібно перебрати можливі варіанти співпадання значень простих суджень не попарно, а для всіх зразу. Наприклад, для приведеного судження табличка виглядала би так:
| A | B | C | D | A→B | С&D | ¬(С&D) | 1ν2 |
| і | і | і | і | і | і | х | і |
| і | і | і | х | і | х | і | і |
| і | і | х | х | і | х | і | і |
| і | х | х | х | х | х | і | і |
| х | х | х | х | і | х | і | і |
| х | х | х | і | х | і | і | |
| х | х | і | і | і | і | х | і |
| х | і | і | і | і | і | х | і |
| х | і | і | х | і | і | х | і |
| і | х | х | і | х | х | і | і |
| х | і | х | і | і | х | і | і |
| і | х | і | х | х | х | і | і |
| х | х | і | х | і | х | і | і |
| і | і | х | і | і | х | і | і |
| х | і | х | х | і | х | і | і |
| і | х | і | і | х | і | х | х |
Як бачите, повна перевірка істинності даного складного судження показала, що насправді воно не є логічним законом. Логічним законом воно було би тільки тоді, коли б в останьому стовпчику всі значення були істинними.
Візьмемо ще один приклад:
¬ ((AÉB) ν ¬(С&D)) É (СnВ)
| A | B | AÉB | C | D | С&D | ¬(С&D) | 1ν2 | ¬(1ν2) | С↔В | ¬(С↔В) | 3→4 |
| і | і | і | і | і | і | х | і | х | і | х | і |
| і | х | х | і | х | х | і | і | х | х | і | і |
| х | і | і | х | і | х | і | і | х | х | і | і |
| х | х | і | х | х | х | і | і | х | і | х | і |
Перевіримо результати за допомогою таблиці, в якій будуть враховані всі можливі варіанти співпадання значень простих суджень:
| A | B | C | D | AÉB | С&D | ¬(С&D) | 1ν2 | ¬(1ν2) | С↔В | ¬(С↔В) | 3→4 |
| і | і | і | і | і | і | х | і | х | і | х | і |
| і | і | і | х | і | х | і | і | х | і | х | і |
| і | і | х | х | і | х | і | і | х | х | і | і |
| і | х | х | х | х | х | і | і | х | х | і | і |
| х | х | х | х | і | і | х | х | і | х | і | і |
| х | х | х | і | х | і | і | х | х | і | і | |
| х | х | і | і | х | і | і | х | і | х | і | |
| х | і | і | і | х | і | і | х | і | х | і | |
| і | х | і | і | х | і | х | і | х | і | ||
| х | і | і | х | х | і | і | х | і | х | і | |
| х | і | х | і | х | і | і | х | х | і | і | |
| х | х | і | х | х | і | і | х | х | і | і | |
| і | і | х | і | і | х | і | х | х | і | і | |
| х | х | і | х | х | і | і | х | х | і | і | |
| і | х | і | і | х | і | і | х | і | х | і | |
| х | і | х | х | х | і | і | х | і | х | і |
В даному випадку перевірка підтвердила результати скороченого методу.
Треба зауважити, що саме цей розділ логіки, який вивчає операції над складними судженнями, ліг в основу сучасного комп'ютерного програмування. Широко використовуються результати і методи цього розділу логіки і в теорії автоматів – в науці, яка складає теоретичну базу конструювання обчислювальної техніки.